Grigory Yakovlevich Perelman có thể được coi là Nhà toán học số 1 thế giới hiện nay, người đã chứng minh giả thuyết Poincaré, một trong bảy bài toán thiên niên kỷ. Ông đã từ chối Huy chương Fields, giải thưởng một triệu đô la Mỹ của Viện toán học Clay, từ chối danh hiệu Viện sĩ Viện Hàn lâm khoa học Liên bang Nga. Để vinh danh ông, người ta đã đặt tên Perelman cho hành tinh nhỏ 50033.

                           Grigory Yakovlevich Perelman

Ảnh: https://avatars.mds.yandex.net/get-zen_doc/1661842

Giả thuyết Poincaré

Henri Poincaré (1854-1912) là nhà toán học, vật lý học, kỹ sư và triết học người pháp. Giả thuyết Poincaré là một bài toán trong lĩnh vực toán topo, tập trung vào các tính chất bên trong của không gian. Đối với các nhà Toán học ngành Topology, đường tròn hay đường cong ellip là như nhau, bởi vì vật thể này có thể biến thành vật thể kia bằng một phép biến hình liên tục (co, kéo, không được cắt, không được xoi lỗ, và không được dán).

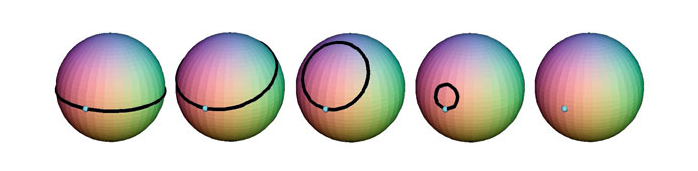
Một vòng dây đàn hồi căng trên mặt cầu hai chiều về mặt lý thuyết có thể được co đến một điểm như mô tả ở hình trên. Bất kỳ bề mặt hai chiều nào không  biên mà trên đó người ta có thể làm như vậy, theo quan điểm của topo học, tương đương với mặt cầu hai chiều. [4]

Poincaré đã sử dụng thuật ngữ "đa tạp" để mô tả các không gian topo trừu tượng này. Khái niệm đa tạp hai chiều hay bề mặt là một đối tượng toán học mà mọi khu vực trên đó có thể biểu diễn bằng một bản đồ nào đó trên một tờ giấy. [1]

Đa tạp hai chiều là đối tượng toán học đã được lý tưởng hóa từ thực tế vật lý. Khi nói Trái Đất là một hình cầu, ta đang nói rằng đối tượng toán học mặt cầu là một mô hình đúng cho bề mặt của Trái Đất. Mặt cầu ở đây có nghĩa là lớp vỏ bên ngoài hay bề mặt.

Hai đa tạp giống nhau về mặt topo học được gọi là đồng phôi.

Hai bề mặt bất kỳ có thể biến đổi để trở nên giống nhau bằng cách kéo dài hoặc nới rộng ra (không xé rách bởi vì làm vậy có thể phá vỡ tính liên tục) là đồng phôi. Ví dụ: Hai mặt cầu có bán kính khác nhau là đồng phôi.

Mặt cầu là một đa tạp 2 chiều hữu hạn. Khối cầu ba chiều hoặc khối cầu bậc 3 là đa tạp bậc 3 hữu hạn đơn giản nhất.

Giả thuyết Poincaré do nhà toán học người  Pháp Henri Poincaréđề xuất vào năm 1904. Giả thuyết Poincaré khẳng định rằng nếu có môt đa tạp bậc 3 hữu hạn mà ở đó, tất cả các mặt kín có thể co rút thành 1 điểm thì đa tạp đó đồng nhất về mặt topo học (nghĩa là đồng phôi) với khối cầu bậc 3. [1]

Có thể diễn đạt bằng các từ ngữ đơn giản giả thuyết Poincaré như sau: “Nếu bề mặt 3 chiều giống khối cầu thì tồn tại khả năng nới rộng nó thành khối cầu’.

Đến năm 1982, giả thuyết Poincaré đã được chứng minh một cách đáng tin cậy cho tất cả các trường hợp ngoại trừ ba chiều.

Ngày 24/05/2000,Viện toán học Clay công bố danh sách 7 bài toán thiên niên kỷ. Đây là những bài toán cổ điển quan trọng, mà đã qua nhiều năm chưa có lời giải. Giả thuyết Poincaré là một trong những bài toán ấy. Viện toán học Clay do doanh nhân Landon T. Clay thành lập năm 1998 tại Cambridge (Mỹ) với mục đích phát triển và phổ biến toán học.

Tuổi học trò

G. Ya. Perelman sinh ngày 13/6/1966 tại Saint-Peterburg trong một gia đình  có nguồn gốc Do Thái, cha là kỹ sư điện, mẹ là giáo viên toán. Perelman đã học tại trường THPTChuyên toán số 239. Năm 1982 là thành viên đoàn học sinh Liên Xô dự Olimpic Toán quốc tế ở Budapest (Hungary), Perelman giành Huy chương Vàng với số điểm đạt tối đa 42/42 (cùng với Bruno Haible của Đức và Lê Tự Quốc Thắng của Việt Nam).

Trong cùng năm đó, anh được tuyển thẳng vào Khoa Toán - Cơ của Đại học Tổng hợp quốc gia Leningrad. Sinh viên Perelman đã giành chiến thắng tất cả các kỳ thi Olympic Toán học cấp khoa, cấp thành phố và cấp liên bang, được trao học bổng Lenin và tốt nghiệp đại học loại giỏi.

Trên đường nghiên cứu toán học

Perelman đã theo chương trình nghiên cứu sinh tại Phân viện Viện toán học. V.A. Steklov tại Saint-Peterburg thuộc Viện Hàn lâm khoa học Liên bang Nga.

Năm 1990,Perelman bảo vệ luận án Tiến sĩ Toán học.

Sau đó Perelman được tiếp nhận làm nghiên cứu viên tại phân viện đã nêu. Tại đây Perelman nghiên cứu và có nhiều công trình về lý thuyết không gian Alexandrov. [2]

Năm 1991,Perelman được trao giải thưởng của Hội Toán học thành phố Saint-Peterburg giành cho các nhà toán học trẻ vì công trình về không gian Alekxandrov.

Năm 1992,Perelman được mời làm việc tại Đại học New York. Một lần sau khi nghe bài giảng về dòng Ricci (Ricci flow) của Richard Hamilton, GS Đại học Columbia, Perelman đã đi đến GS này và trò chuyện. Perelman nhớ lại: “Tôi rất muốn hỏi ông ấy điều gì đó. Ông ấy cười và rất kiên nhẫn nghe tôi nói. Ông ấy thậm chí còn thổ lộ với tôi một số vấn đề mà vài năm sau ông mới công bố. Ông không ngần ngại mà đã chia sẻ với tôi. Tôi rất thích tính cởi mở và hào phóng của ông. Tôi có thể nói rằng về mặt này Hamilton không hề giống như phần lớn các nhà toán học khác”. [4]

Năm 1982, Hamilton đã công bố bài báo về một phương trình gọi là dòng Ricci (Ricci flow), đó là công cụ chính để chứng minh giả thuyết Poincaré.

Năm 1993, Perelman đã giải quyết một bài toán quan trọng và  cực kỳ khó, mà hai mươi năm trước Jeff Cheeger và Detler Gromol đặt ra, gọi là giả thuyết Soul (Soul Conjecture). Các nhà toán học đã nhận xét lời giải của Perelman "đẹp ngoạn mục",  trình bày trong bài viết chỉ có bốn trang. [7]

Năm 1993,Perelman nhận được học bổng Miller Research Fellowship 2 năm tại Đại học California ở Berkeley.

Năm 1994,Perelman được mời phát biểu trước Đại hội toán học thế giới (CMI-1994) ở Zurich (Thụy sĩ). Đây là một vinh dự lớn cho nhà toán học xuất sắc.

Trong thời gian này,được mời cộng tác với những trường đại học hàng đầu của Mỹ như Đại học Princeton, Đại học Stanford nhưng Perelman từ chối mọi đề nghị. Vào mùa hè năm 1995,trở về Viện toán học Steklov, ông bắt đầu tập trung nghiên cứu về dòng Ricci mà Hamilton đã đề xuất. [5]

Năm 1996,được Hội Toán học châu Âu tặng giải thưởng cho nhà toán học trẻ nhưng Perelman từ chối nhận.

Khi đã đạt được một số thành công trong nghiên cứu ý tưởng mà Hamilton đã thổ lộ, Perelman viết thư cho Hamilton với đề nghị hợp tác nghiên cứu nhưng ông này không trả lời.

Ngày 11/11/2002, Perelman đã đăng bài báo có tựa đề “Công thức Entropy cho dòng Ricci và các ứng dụng hình học của nó” (“The Entropy Formula for the Ricci Flow and Its Geometric Applications”), dài 39 trang trên trang web www.arXiv.org, nơi đăng các bài báo đang chờ công bố chính thức trên các tạp chí chuyên ngành.

Ngày10/03/2003,Perelman đăng bài thứ hai (“Ricci flow with  surgey on three-manifolds”) dài 22 trang và ngày 17/07/2003 đăng bài thứ ba (“Finite extintion times for the solutions to the Ricci flow on certain three-manifolds”)  chỉ dài 7 trang.

Ngay sau đó nhiều nhóm độc lập với nhau, gồm các nhà toán học tài năng đã làm việc nghiên cứu, kiểm tra lại công trình của Perelman đã công bố, như: 1) John Morgan thuộc Đại học Columbia và Tian Gang (Điền Cương) thuộc Viện MIT (Massachusetts Institute of Technology), 2) Bruce Kleiner và John Lott thuộc Đại học Michigan, 3) Cao Huai-Dong (Tào Hoài Đồng) thuộc Đại học Lehigh Pennsylvania và Zhu XiPing (Chu Hi Bình) thuộc Đại học Sun Yat-Sen (Tôn Dật Tiên). Mùa hè năm 2006,kết quả của các nhóm được công bố với kết luận là công trình của Perelman hoàn toàn đúng.

Có một âm mưu?

Một nhóm các nhà toán học Trung-Mỹ tự cho mình mới chính là người tạo ra bước quyết định trong việc chứng minh giả thuyết Poincaré chứ không phải Perelman, trong đó Yau Shing-Tung là người chủ trò. Yau Shing-Tung là một nhà Toán học gốc Trung Hoa, làm việc tại Viện Nghiên cứu Cao cấp Princeton và giảng dạy tại nhiều trường Đại học nổi tiếng khác. Với nhiều đóng góp cho Toán học, Yau được tặng Huy chương Fields năm 1982 và nhiều giải thưởng khác.

Tạp chí The Asian Journal of Mathematics (mà Yau là một biên tập viên) số 6/2006 (Asian Journal of Mathematics. Vol. 10, No. 2, pp. 165-492, June 2006) đã đăng bài báo của Cao Huai-Dong và Zhu Xi-Ping, là hai sinh viên của Yau dài 327 trang với tiêu đề “Chứng minh đầy đủ cho giả thuyết Poincaré và hình học hóa - áp dụng lý thuyết dòng Ricci của Hamilton và Perelman”. [2]

Vào ngày 03/6/2006, Yau đã triệu tập một cuộc họp báo tại Viện Toán học ở Bắc Kinh và tuyên bố: "Đóng góp của Hamilton cho chứng minh [giả thuyết Poincaré] là khoảng 50%, của Perelman người Nga là khoảng 25%, của Yau, Zhu, Cao và những người khác là khoảng 30%." [7]

Thật đáng ngạc nhiên vì thông điệp này cho kết quả phép tính là 105%.

Các nhà toán học nổi tiếng khác đã khảo sát chứng minh của Perelman, bác bỏ ý kiến ​​cho rằng Zhu và Cao đã đóng góp những cách tiếp cận mới đáng kể cho việc chứng minh giả thuyết Poincaré. Trong bài báo đăng trên tờ The New Yorker nhà toán học John Morgan nhận xét: “Tôi không thấy họ [Zhu và Cao] làm gì khác [so với Perelman] cả.”

Có ý kiến cho rằng Yau Shing-Tung âm mưu giật Huy chương Fields của Perelman để bản thân được coi là vua ngành hình học?

Đúng vào ngày khai mạc Đại hội Toán học thế giới ICM-2006 tại Madrit (Tây Ban Nha),tờ The New Yorker số ra ngày 22/08/2006, đăng một bài báo của Sylvia Nasar và David Gruber tiêu đề “Manifold destiny: A legendarny problem and the battle over who solved it”. (Số phận đa dạng: Bài toán khó huyền thoại và cuộc chiến về người giải nó). Ngoài phần phỏng vấn đặc biệt với Perelman, bài báo kể lại sự tham gia của Yau vào chuyện chê bai công trình của Perelman cùng với âm mưu có thể có, đã mô tả Yau là rất có khả năng chuyên môn, kiêu ngạo, tranh đấu cho vị trí và danh tiếng của mình, bài có hình minh họa Yau cố kéo cái Huy chương Fields đeo ở cổ Perelman. [6]

Khi các phóng viên hỏi, ông nghĩ gì về việc làm của các nhà toán học Trung Quốc, Perelman trả lời: “Không thể nói rằng tôi phẫn nộ, những người khác còn lại hành động tồi tệ hơn. Tất nhiên, nhiều nhà toán học nói chung là trung thực. Nhưng hầu như tất cả trong số họ là người dĩ hòa vi quý. Bản thân họ là trung thực, nhưng họ chấp nhận những người không trung thực”. Sau đó, ông lưu ý một cách cay đắng: “Những người vi phạm các tiêu chuẩn đạo đức trong khoa học không bị coi là lạc lõng, mà [ngược lại] những người như tôi lại bị cô lập”. [4]

Đại hội Toán học thế giới năm 2006 (ICM-2006)

CM-2006 được tổ chức vào tháng 8/2006 ở Madrid (Tây Ban Nha).

Công trình chứng minh giả thuyết Poincaré là một nội dung chính được thảo luận trong Đại hội IMC-2006.

Trong Diễn văn khai mạc Đại hội ICM-2006,Ngài John Ball, GS Đại học Oxford, Chủ tịch Hội Toán học thế giới (IMU) có đoạn: “Toán học là một nghề của những tiêu chuẩn cao sang và sự liêm chính. Chúng ta bàn luận một cách thoải mái công việc của mình với người khác mà không sợ bị đánh cắp, và các nghiên cứu được trao đổi một cách cởi mở trước khi công bố chính thức. Các quá trình biên tập luôn công bằng và đúng, và các công trình đạt được tiếng tăm của chúng qua sự xứng đáng chứ không phải bằng cách thức nâng đỡ. Đây là những tiêu chuẩn mà đại đa số các nhà toán học làm theo. Ngoại lệ rất hiếm, và chúng sẽ bị nhận ra.”[1]

Tại ICM-2006, IMU đã công bố quyết định tặng Huy chương Fields cho bốn nhà toán học gồm: Andrei Okounkov, Grigory Perelman, Terence Tao và Wendelin Werner.

Năm 2010, Viện Clay đã tổ chức trao cho Perelman giải thưởng triệu đô về công trình chứng minh giả thuyết Poincaré nhưng Nhà toán học từ chối giải thưởng này và không đến Paris dự lễ vì người ta chỉ trao thưởng cho ông mà không chia phần cho Hamilton.

Vậy Perelman là người thế nào?

Ta có thể nhận thấy rằng: 1) Perelman là người có trí tuệ siêu việt. Qua gần một thế kỷ nhiều nhà toán học xuất sắc đã bỏ công nghiên cứu chứng minh giả thuyết Poincaré nhưng không người nào đi đến kết quả; trong vòng 7 năm Perelman đã hoàn thành xuất sắc công trình vĩ đại chứng minh giả thuyết hình học hóa, trong đó giả thuyết Poincaré là một trường hợp; 2) Perelman là người không chạy theo tiền bạc. Có ý kiến cho rằng, Perelman cố chứng minhgiả thuyết Poincaré để có 1 triệu USD của Viện toán học Clay. Đó là điều dối trá. Năm 2000 Viện này mới đề xuất 7 bài toán thiên niên kỷ và giải thường nhưng Perelman đã bắt đầu nghiên cứu giả thuyết Poincaré từ năm 1995.Vào năm 2004,lương của Nghiên cứu viên chính như Perelman vào khoảng 400 USD (đã cao hơn nhiều so với những năm đầu 1990). Nếu như Perelman có học vị Tiến sĩ khoa học thì lương sẽ cao hơn nữa nhưng ông không quan tâm đến điều đó.Việc từ chối lời mời làm việc ở các trường Đại học hàng đầu của Mỹ cũng là một minh chứng điều đó; 3) Perelman là người không tham danh vọng. Nhiều khi Perelman không hứng thú công bố công trình nghiên cứu của mình mà chỉ thông báo cho bạn bè. Perelman đã từ chối Huy chương Fields, giải thưởng của Hội toán học châu Âu, từ chối làm thủ tục bầu Viện sĩ Viện hàn lâm khoa học Liên bang Nga; 4) Perelman là người khiêm tốn. Tuy đạt được đỉnh cao mà Hamilton hằng mơ ước nhưng Perelman vẫn coi Hamilton là thấy của mình. Perelman là người rất nghiêm túc tôn trọng bản quyền (được biết trong phần tham khảo của bài báo thứ nhất ông đã ghi 10 bài báo, trong bài thứ hai ghi 5 bài báo của Hamilton); 5) Perelman là thiên tài người lập dị. Công trình chứng minh giả thuyết Poincaré là công sức 7 năm làm việc cật lực, kết quả có ý nghĩa to lớn đáng ra phải đăng trên một tờ báo chuyên ngành để được các chuyên gia toán học hàng đầu bình duyệt và công nhận nhưng Perelman chỉ đăng trên trang web thông tin khoa học bình thường. Trong ba bài báo đã nêu dài 67 trang (trong đó phần quan trọng nhất ở bài báo thứ ba chỉ có 7 trang), được trình bày hết sức cô động, ít dẫn dắt làm cho người đọc là những nhà toán học xuất sắc  cũng rất tốn công sức và thời gian trong việc tìm hiểu và truyền đạt lại cho người khác.Câu trả lời của Perelman khi được phỏng vấn cũng thật khác người: “Tôi không quan tâm đến tiền bạc và danh vọng. Tôi không muốn bị coi như con thú trong vườn bách thú”.

Thay lời kết luận

Công trình của Perelman là thành tự to lớn của lịch sử toán học, không chỉ chứng minh giả thuyết Poincaré, mà còn cả giả thuyết Hình học hóa Thurton. “Giả thuyết Poincaré được gọi là “Công thức của Vũ trụ” vì tầm quan trọng của nó trong nghiên cứu các quá trình vật lý phức tạp trong lý thuyết vũ trụ và bởi vì nó đưa ra câu trả lời về hình dạng của Vũ trụ. Chứng minh này sẽ đóng vai trò lớn trong sự phát triển của công nghệ nano” (Perelman).

Thiên tài và những người tài nói chung thường suy nghĩ độc lập, phong cách  khác người. “Hiền tài là nguyên khí quốc gia” (Thân Nhân Trung), họ có vai trò cực kỳ quan trọng trong sự nghiệp xây dựng và bảo vệ Tổ quốc, luôn sẵn sàng cống hiến tài năng lực cho khoa học, cho đất nước. Vì vậy Nhà nước, các cơ quan nghiên cứu khoa học và đào tạo cần có chính sách, cơ chế bồi dưỡng, thu hút, trọng dụng và đãi ngộ người tài, đảm bảo điều kiện cho họ làm việc hiệu quả nhất.

Từ câu chuyện về thiên tài lập dị Perelman có thể nói rằng, các nhà khoa học trẻ có thể không cần chạy theo số lượng công trình để công bố mà có thể đi thẳng vào những vấn đề hắc búa nhất của khoa học công nghệ, giải quyết những vấn đề thiết yếu do cuộc sống đặt ra./.

TÀI LIỆU THAM KHẢO

1. Donal O’sheha (2012). “Giả thuyết Poincaré. Cuộc tìm kiếm hình dạng vũ trụ”, NXB Tri thức, Hà Nội.

2. https://www.litmir.me/br/?b=215562&p=1, (18.04.2020), Aрсенов Олег. “Григорий Перельман и гипотеза Пуанкаре”. Royalib.com.book/ arsenov…Perelman.

3. https://www.limir.me/br,(19.04.2020) Гесен Мария Александровна. «Совершенная строгость. Григорий Перельман: гений и задача тысяелетия».

4.9https://elementy.ru/nauchno-populyarnaya_biblioteka/434231/ (19.04.2020), Skazka_o_matematike_Grigorii_Perelmane_kotoryy_reshil_odnu_iz_semi_zadach_tysyacheletiya, “Сказка о математике Григории Перельмане, который решил одну из семи задач тысячелетия”.

5. https://lenta.ru/lib/14160587/         9, (19.04.2020) Перельман, Григорий

6. http://www.newyorker.com/archive/2006/08/28/060828fa_fact2(19.04.2020), Sylva Nasar, David  Gruber. "Manifold Destiny: A legendary problem and the battle over who solved it",

7. http://www.astrokras.narod.ru/pub/perelman-1.htm(19.04.2020),

Буралков А.А., “Феномен Григория Перемельна в свете астрологии”.